torchbox.dsp package

Submodules

torchbox.dsp.convolution module

torchbox.dsp.convolution.convn(A, B, dim=0, shape='full', **kwargs)

convolution

Parameters:

  • A (tensor) – input

  • B (tensor) – kernel

  • dim (int, list or tuple, optional) – convolution dim, by default 0

  • shape (str, optional) – convolution shape mode, 'same', 'valid' or 'full', by default 'full'

  • dimb (int, list or tuple) – (kwargs) convolution dim of B, if specified, dim only represents the convolution dim of A

  • bias (bool or None) – (kwargs) with bias? by default None

  • stride (int, list or tuple) – (kwargs) convolution stride

  • padmode (str) – (kwargs) pad mode 'constant' (default), 'reflect', 'replicate'

  • padvalue (float) – (kwargs) pad value

  • dilation (int) – (kwargs) by default 1

  • groups (int) – (kwargs) by default 1

torchbox.dsp.convolution.cutfftconv1(y, nfft, Nx, Nh, shape='same', dim=0, ftshift=False)

Throwaway boundary elements to get convolution results.

Throwaway boundary elements to get convolution results.

Parameters:

  • y (Tensor) – array after iff.

  • nfft (int) – number of fft points.

  • Nx (int) – signal length

  • Nh (int) – filter length

  • shape (str) – output shape: 1. 'same' --> same size as input x, \(N_x\) 2. 'valid' --> valid convolution output 3. 'full' --> full convolution output, \(N_x+N_h-1\) (the default is ‘same’)

  • dim (int) – convolution dimension (the default is 0)

  • ftshift (bool) – whether to shift zero the frequency to center (the default is False)

Returns:

y – array with shape specified by same.

Return type:

Tensor

torchbox.dsp.convolution.fftconv1(x, h, shape='same', nfft=None, ftshift=False, eps=None, **kwargs)

Convolution using Fast Fourier Transformation

Convolution using Fast Fourier Transformation.

Parameters:

  • x (Tensor) – data to be convolved.

  • h (Tensor) – filter array

  • shape (str, optional) – output shape: 1. 'same' --> same size as input x, \(N_x\) 2. 'valid' --> valid convolution output 3. 'full' --> full convolution output, \(N_x+N_h-1\) (the default is ‘same’)

  • cdim (int or None) – If x is complex-valued, cdim is ignored. If x is real-valued and cdim is integer then x will be treated as complex-valued, in this case, cdim specifies the complex dim; otherwise (None), x will be treated as real-valued.

  • dim (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

  • nfft (int, optional) – number of fft points (the default is \(2^{nextpow2(N_x+N_h-1)}\)), note that nfft can not be smaller than \(N_x+N_h-1\).

  • ftshift (bool, optional) – whether shift frequencies (the default is False)

  • eps (None or float, optional) – x[abs(x)<eps] = 0 (the default is None, does nothing)

Returns:

y – Convolution result array.

Return type:

Tensor

torchbox.dsp.correlation module

torchbox.dsp.correlation.accc(Sr, isplot=False)

Average cross correlation coefficient

Average cross correlation coefficient (ACCC)

\[\overline{C(\eta)}=\sum_{\eta} s^{*}(\eta) s(\eta+\Delta \eta) \]

where, \(\eta, \Delta \eta\) are azimuth time and it’s increment.

Parameters:

Sr (numpy array) – SAR raw signal data \(N_a×N_r\) or range compressed data.

Returns:

ACCC in each range cell.

Return type:

1d array

torchbox.dsp.correlation.acorr(x, P, dim=0, scale=None)

computes auto-correlation using fft

Parameters:

  • x (Tensor) – the input signal tensor

  • P (int) – maxlag

  • dim (int) – the auto-correlation dimension

  • scale (str or None, optional) – None, 'biased' or 'unbiased', by default None

torchbox.dsp.correlation.cutfftcorr1(y, nfft, Nx, Nh, shape='same', dim=0, ftshift=False)

Throwaway boundary elements to get correlation results.

Throwaway boundary elements to get correlation results.

Parameters:

  • y (Tensor) – array after iff.

  • nfft (int) – number of fft points.

  • Nx (int) – signal length

  • Nh (int) – filter length

  • shape (dstr) – output shape: 1. 'same' --> same size as input x, \(N_x\) 2. 'valid' --> valid correlation output 3. 'full' --> full correlation output, \(N_x+N_h-1\) (the default is ‘same’)

  • dim (int) – correlation dim (the default is 0)

  • ftshift (bool) – whether to shift the frequencies (the default is False)

Returns:

y – array with shape specified by same.

Return type:

Tensor

torchbox.dsp.correlation.fftcorr1(x, h, shape='same', nfft=None, ftshift=False, eps=None, **kwargs)

Correlation using Fast Fourier Transformation

Correlation using Fast Fourier Transformation.

Parameters:

  • x (Tensor) – data to be convolved.

  • h (Tensor) – filter array, it will be expanded to the same dimensions of x first.

  • shape (dstr, optional) – output shape: 1. 'same' --> same size as input x, \(N_x\) 2. 'valid' --> valid correlation output 3. 'full' --> full correlation output, \(N_x+N_h-1\) (the default is ‘same’)

  • cdim (int or None) – If x is complex-valued, cdim is ignored. If x is real-valued and cdim is integer then x will be treated as complex-valued, in this case, cdim specifies the complex dim; otherwise (None), x will be treated as real-valued.

  • dim (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

  • nfft (int, optional) – number of fft points (the default is None, \(2^{nextpow2(N_x+N_h-1)}\)), note that nfft can not be smaller than \(N_x+N_h-1\).

  • ftshift (bool, optional) – whether shift frequencies (the default is False)

  • eps (None or float, optional) – x[abs(x)<eps] = 0 (the default is None, does nothing)

Returns:

y – Correlation result array.

Return type:

Tensor

torchbox.dsp.correlation.xcorr(A, B, shape='same', dim=0)

Cross-correlation function estimates.

Parameters:

  • A (numpy array) – data1

  • B (numpy array) – data2

  • mod (str, optional) –

    • ‘biased’: scales the raw cross-correlation by 1/M.

    • ’unbiased’: scales the raw correlation by 1/(M-abs(lags)).

    • ’coeff’: normalizes the sequence so that the auto-correlations

      at zero lag are identically 1.0.

    • ’none’: no scaling (this is the default).

torchbox.dsp.ffts module

torchbox.dsp.ffts.fft(x, n=None, norm='backward', shift=False, **kwargs)

FFT in torchbox

FFT in torchbox, both real and complex valued tensors are supported.

Parameters:

  • x (Tensor) – When x is complex, it can be either in real-representation format or complex-representation format.

  • n (int, optional) – The number of fft points (the default is None –> equals to signal dimension)

  • norm (None or str, optional) – Normalization mode. For the forward transform (fft()), these correspond to: “forward” - normalize by 1/n; “backward” - no normalization (default); “ortho” - normalize by 1/sqrt(n) (making the FFT orthonormal).

  • shift (bool, optional) – shift the zero frequency to center (the default is False)

  • cdim (int or None) – If x is complex-valued, cdim is ignored. If x is real-valued and cdim is integer then x will be treated as complex-valued, in this case, cdim specifies the complex dimension; otherwise (None), x will be treated as real-valued.

  • dim (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

Returns:

y – fft results tensor with the same type as x

Return type:

Tensor

Raises:

ValueError – nfft is small than signal dimension.

:raises see also ifft(), fftfreq(), freq().:

Examples

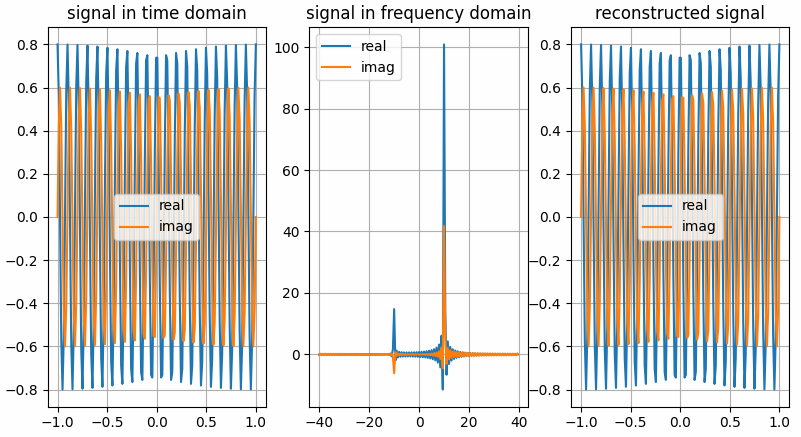
_images/FFTIFFTdemo.png

The results shown in the above figure can be obtained by the following codes.

import torch as th
import torchbox as tb
import matplotlib.pyplot as plt

shift = True
frq = [10, 10]
amp = [0.8, 0.6]
Fs = 80
Ts = 2.
Ns = int(Fs * Ts)

t = th.linspace(-Ts / 2., Ts / 2., Ns).reshape(Ns, 1)
f = tb.freq(Ns, Fs, shift=shift)
f = tb.fftfreq(Ns, Fs, norm=False, shift=shift)

# ---complex vector in real representation format
x = amp[0] * th.cos(2. * th.pi * frq[0] * t) + 1j * amp[1] * th.sin(2. * th.pi * frq[1] * t)

# ---do fft
Xc = tb.fft(x, n=Ns, cdim=None, dim=0, shift=shift)

# ~~~get real and imaginary part
xreal = tb.real(x, cdim=None, keepdim=False)
ximag = tb.imag(x, cdim=None, keepdim=False)
Xreal = tb.real(Xc, cdim=None, keepdim=False)
Ximag = tb.imag(Xc, cdim=None, keepdim=False)

# ---do ifft
x̂ = tb.ifft(Xc, n=Ns, cdim=None, dim=0, shift=shift)

# ~~~get real and imaginary part
x̂real = tb.real(x̂, cdim=None, keepdim=False)
x̂imag = tb.imag(x̂, cdim=None, keepdim=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()

# ---complex vector in real representation format
x = tb.c2r(x, cdim=-1)

# ---do fft
Xc = tb.fft(x, n=Ns, cdim=-1, dim=0, shift=shift)

# ~~~get real and imaginary part
xreal = tb.real(x, cdim=-1, keepdim=False)
ximag = tb.imag(x, cdim=-1, keepdim=False)
Xreal = tb.real(Xc, cdim=-1, keepdim=False)
Ximag = tb.imag(Xc, cdim=-1, keepdim=False)

# ---do ifft
x̂ = tb.ifft(Xc, n=Ns, cdim=-1, dim=0, shift=shift)

# ~~~get real and imaginary part
x̂real = tb.real(x̂, cdim=-1, keepdim=False)
x̂imag = tb.imag(x̂, cdim=-1, keepdim=False)

plt.figure()
plt.subplot(131)
plt.grid()
plt.plot(t, xreal)
plt.plot(t, ximag)
plt.legend(['real', 'imag'])
plt.title('signal in time domain')
plt.subplot(132)
plt.grid()
plt.plot(f, Xreal)
plt.plot(f, Ximag)
plt.legend(['real', 'imag'])
plt.title('signal in frequency domain')
plt.subplot(133)
plt.grid()
plt.plot(t, x̂real)
plt.plot(t, x̂imag)
plt.legend(['real', 'imag'])
plt.title('reconstructed signal')
plt.show()
torchbox.dsp.ffts.fftfreq(n, fs, norm=False, shift=False, dtype=torch.float32, device='cpu')

Return the Discrete Fourier Transform sample frequencies

Return the Discrete Fourier Transform sample frequencies.

Given a window length n and a sample rate fs, if shift is True:

f = [-n/2, ..., -1,     0, 1, ...,   n/2-1] / (d*n)   if n is even
f = [-(n-1)/2, ..., -1, 0, 1, ..., (n-1)/2] / (d*n)   if n is odd

Given a window length n and a sample rate fs, if shift is False:

f = [0, 1, ...,   n/2-1,     -n/2, ..., -1] / (d*n)   if n is even
f = [0, 1, ..., (n-1)/2, -(n-1)/2, ..., -1] / (d*n)   if n is odd

If norm is True, \(d = 1\), else \(d = 1/f_s\).

Parameters:

  • n (int) – Number of samples.

  • fs (float) – Sampling rate.

  • norm (bool) – Normalize the frequencies.

  • shift (bool) – Does shift the zero frequency to center.

  • dtype (torch tensor type) – Data type, default is th.float32.

  • device (torch device) – device string, 'cpu', 'cuda:0', 'cuda:1'

Returns:

Frequency array with size \(n×1\).

Return type:

torch 1d-array

Examples

import torchbox as tb

n = 10
print(np.fft.fftfreq(n, d=0.1), 'numpy')
print(th.fft.fftfreq(n, d=0.1), 'torch')
print(tb.fftfreq(n, fs=10., norm=False), 'fftfreq, norm=False, shift=False')
print(tb.fftfreq(n, fs=10., norm=True), 'fftfreq, norm=True, shift=False')
print(tb.fftfreq(n, fs=10., shift=True), 'fftfreq, norm=False, shift=True')
print(tb.freq(n, fs=10., norm=False), 'freq, norm=False, shift=False')
print(tb.freq(n, fs=10., norm=True), 'freq, norm=True, shift=False')
print(tb.freq(n, fs=10., shift=True), 'freq, norm=False, shift=True')

# ---output
[ 0.  1.  2.  3.  4. -5. -4. -3. -2. -1.] numpy
tensor([ 0.,  1.,  2.,  3.,  4., -5., -4., -3., -2., -1.]) torch
tensor([ 0.,  1.,  2.,  3.,  4., -5., -4., -3., -2., -1.]) fftfreq, norm=False, shift=False
tensor([ 0.0000,  0.1000,  0.2000,  0.3000,  0.4000, -0.5000, -0.4000, -0.3000,
        -0.2000, -0.1000]) fftfreq, norm=True, shift=False
tensor([-5., -4., -3., -2., -1.,  0.,  1.,  2.,  3.,  4.]) fftfreq, norm=False, shift=True
tensor([ 0.0000,  1.1111,  2.2222,  3.3333,  4.4444,  5.5556,  6.6667,  7.7778,
        8.8889, 10.0000]) freq, norm=False, shift=False
tensor([0.0000, 0.1111, 0.2222, 0.3333, 0.4444, 0.5556, 0.6667, 0.7778, 0.8889,
        1.0000]) freq, norm=True, shift=False
tensor([-5.0000, -3.8889, -2.7778, -1.6667, -0.5556,  0.5556,  1.6667,  2.7778,
        3.8889,  5.0000]) freq, norm=False, shift=True
torchbox.dsp.ffts.fftshift(x, **kwargs)

Shift the zero-frequency component to the center of the spectrum.

This function swaps half-spaces for all axes listed (defaults to all). Note that y[0] is the Nyquist component only if len(x) is even.

Parameters:

  • x (Tensor) – Input tensor.

  • dim (int, optional) – Axes over which to shift. (Default is None, which shifts all axes.)

Returns:

y – The shifted tensor.

Return type:

Tensor

See also

ifftshift

The inverse of fftshift.

Examples

import numpy as np
import torch as th
import torchbox as tb

x = [1, 2, 3, 4, 5, 6]
y = np.fft.fftshift(x)
print(y)
x = th.tensor(x)
y = tb.fftshift(x)
print(y)

x = [1, 2, 3, 4, 5, 6, 7]
y = np.fft.fftshift(x)
print(y)
x = th.tensor(x)
y = tb.fftshift(x)
print(y)

dim = (0, 1)  # dim = 0, dim = 1
x = [[1, 2, 3, 4, 5, 6], [0, 2, 3, 4, 5, 6]]
y = np.fft.fftshift(x, dim)
print(y)
x = th.tensor(x)
y = tb.fftshift(x, dim)
print(y)

x = [[1, 2, 3, 4, 5, 6, 7], [0, 2, 3, 4, 5, 6, 7]]
y = np.fft.fftshift(x, dim)
print(y)
x = th.tensor(x)
y = tb.fftshift(x, dim)
print(y)
torchbox.dsp.ffts.freq(n, fs, norm=False, shift=False, dtype=torch.float32, device='cpu')

Return the sample frequencies

Return the sample frequencies.

Given a window length n and a sample rate fs, if shift is True:

f = [-n/2, ..., n/2] / (d*n)

Given a window length n and a sample rate fs, if shift is False:

f = [0, 1, ..., n] / (d*n)

If norm is True, \(d = 1\), else \(d = 1/f_s\).

Parameters:

  • fs (float) – Sampling rate.

  • n (int) – Number of samples.

  • norm (bool) – Normalize the frequencies.

  • shift (bool) – Does shift the zero frequency to center.

  • dtype (torch tensor type) – Data type, default is th.float32.

  • device (str) – device string, default is 'cpu'.

Returns:

Frequency array with size \(n×1\).

Return type:

torch 1d-tensor

Examples

import torchbox as tb

n = 10
print(np.fft.fftfreq(n, d=0.1), 'numpy')
print(th.fft.fftfreq(n, d=0.1), 'torch')
print(tb.fftfreq(n, fs=10., norm=False), 'fftfreq, norm=False, shift=False')
print(tb.fftfreq(n, fs=10., norm=True), 'fftfreq, norm=True, shift=False')
print(tb.fftfreq(n, fs=10., shift=True), 'fftfreq, norm=False, shift=True')
print(tb.freq(n, fs=10., norm=False), 'freq, norm=False, shift=False')
print(tb.freq(n, fs=10., norm=True), 'freq, norm=True, shift=False')
print(tb.freq(n, fs=10., shift=True), 'freq, norm=False, shift=True')

# ---output
[ 0.  1.  2.  3.  4. -5. -4. -3. -2. -1.] numpy
tensor([ 0.,  1.,  2.,  3.,  4., -5., -4., -3., -2., -1.]) torch
tensor([ 0.,  1.,  2.,  3.,  4., -5., -4., -3., -2., -1.]) fftfreq, norm=False, shift=False
tensor([ 0.0000,  0.1000,  0.2000,  0.3000,  0.4000, -0.5000, -0.4000, -0.3000,
        -0.2000, -0.1000]) fftfreq, norm=True, shift=False
tensor([-5., -4., -3., -2., -1.,  0.,  1.,  2.,  3.,  4.]) fftfreq, norm=False, shift=True
tensor([ 0.0000,  1.1111,  2.2222,  3.3333,  4.4444,  5.5556,  6.6667,  7.7778,
        8.8889, 10.0000]) freq, norm=False, shift=False
tensor([0.0000, 0.1111, 0.2222, 0.3333, 0.4444, 0.5556, 0.6667, 0.7778, 0.8889,
        1.0000]) freq, norm=True, shift=False
tensor([-5.0000, -3.8889, -2.7778, -1.6667, -0.5556,  0.5556,  1.6667,  2.7778,
        3.8889,  5.0000]) freq, norm=False, shift=True
torchbox.dsp.ffts.ifft(x, n=None, norm='backward', shift=False, **kwargs)

IFFT in torchbox

IFFT in torchbox, both real and complex valued tensors are supported.

Parameters:

  • x (Tensor) – When x is complex, it can be either in real-representation format or complex-representation format.

  • n (int, optional) – The number of ifft points (the default is None –> equals to signal dimension)

  • norm (bool, optional) –

    Normalization mode. For the backward transform (ifft()), these correspond to: “forward” - no normalization;

    ”backward” - normalize by 1/n (default); “ortho” - normalize by 1``/sqrt(n)`` (making the IFFT orthonormal).

  • shift (bool, optional) – shift the zero frequency to center (the default is False)

  • cdim (int or None) – If x is complex-valued, cdim is ignored. If x is real-valued and cdim is integer then x will be treated as complex-valued, in this case, cdim specifies the complex axis; otherwise (None), x will be treated as real-valued.

  • dim (int, optional) – axis of fft operation (the default is 0, which means the first dimension)

Returns:

y – ifft results tensor with the same type as x

Return type:

Tensor

Raises:

ValueError – nfft is small than signal dimension.

:raises see also fft(), fftfreq(), freq(). see also fft() for examples.:

torchbox.dsp.ffts.ifftshift(x, **kwargs)

Shift the zero-frequency component back.

The inverse of fftshift. Although identical for even-length x, the functions differ by one sample for odd-length x.

Parameters:

  • x (Tensor) – The input tensor.

  • dim (int, optional) – Axes over which to shift. (Default is None, which shifts all axes.)

Returns:

y – The shifted tensor.

Return type:

Tensor

See also

fftshift

The inverse of ifftshift.

Examples

import numpy as np
import torch as th
import torchbox as tb

x = [1, 2, 3, 4, 5, 6]
y = np.fft.fftshift(x)
print(y)
x = th.tensor(x)
y = tb.fftshift(x)
print(y)

x = [1, 2, 3, 4, 5, 6, 7]
y = np.fft.fftshift(x)
print(y)
x = th.tensor(x)
y = tb.fftshift(x)
print(y)

dim = (0, 1)  # dim = 0, dim = 1
x = [[1, 2, 3, 4, 5, 6], [0, 2, 3, 4, 5, 6]]
y = np.fft.fftshift(x, dim)
print(y)
x = th.tensor(x)
y = tb.fftshift(x, dim)
print(y)

x = [[1, 2, 3, 4, 5, 6, 7], [0, 2, 3, 4, 5, 6, 7]]
y = np.fft.fftshift(x, dim)
print(y)
x = th.tensor(x)
y = tb.fftshift(x, dim)
print(y)
torchbox.dsp.ffts.padfft(X, nfft=None, dim=0, shift=False)

PADFT Pad array for doing FFT or IFFT

PADFT Pad array for doing FFT or IFFT

Parameters:

  • X (Tensor) – Data to be padded.

  • nfft (int or None) – Padding size.

  • dim (int, optional) – Padding dimension. (the default is 0)

  • shift (bool, optional) – Whether to shift the frequency (the default is False)

Returns:

y – The padded tensor.

Return type:

Tensor

torchbox.dsp.find_peaks module

torchbox.dsp.find_peaks.filtpeaks(ppos, data, dim=-1, hmin=None, dmin=None, issort=True, returns=['pos', 'value'])

filter peaks by height and distance

Parameters:

  • ppos (Tensor) – peaks positions (N x D)

  • data (Tensor) – the data tensor (N x S1 x S2 x … x SD)

  • dim (int or list, optional) – the number of dimensions should be equal to D, by default -1

  • hmin (float or None, optional) – the minimum height of peak, by default None

  • dmin (int, float or None, optional) – the minimum distance between two nearby peaks, by default None

  • issort (bool, optional) – sort peaks according to peak’s values before remove the peaks that does not satisfy the minimum distance constraint, by default True

  • returns (list, optional) – the variables to be returned, by default [‘pos’, ‘value’]

Examples

x = th.zeros(100, )
x[10] = 1.
x[30] = 1.2
x[32] = 0.9
x[34] = 1.1
x[90] = 0.3

ppos = localmax1d(x, win=3, thresh=None)
print(ppos)
print(filtpeaks(ppos, x, dim=0, hmin=0.5, dmin=1))
print(filtpeaks(ppos, x, dim=0, hmin=0.3, dmin=3))

x = th.zeros(60, 70, 80)
x[1, 20, 3] = 1.
x[2, 3, 20] = 0.5
x[2, 5, 20] = 1.3
x[2, 8, 20] = 0.3
ppos = localmax3d(x, win=3, thresh=None)
print(ppos)
print(filtpeaks(ppos, x, dim=[0, 1, 2], hmin=0.5, dmin=1))
print(filtpeaks(ppos, x, dim=[0, 1, 2], hmin=0.3, dmin=3))

# outputs:
tensor([10, 30, 32, 34, 90])
[tensor([30, 34, 10, 32]), tensor([1.2000, 1.1000, 1.0000, 0.9000])]
[tensor([30, 34, 10, 90]), tensor([1.2000, 1.1000, 1.0000, 0.3000])]
tensor([[ 1, 20,  3],
        [ 2,  3, 20],
        [ 2,  5, 20],
        [ 2,  8, 20]])
[tensor([[ 2,  5, 20],
        [ 1, 20,  3],
        [ 2,  3, 20]]), tensor([1.3000, 1.0000, 0.5000])]
[tensor([[ 2,  5, 20],
        [ 1, 20,  3],
        [ 2,  8, 20]]), tensor([1.3000, 1.0000, 0.3000])]
torchbox.dsp.find_peaks.findpeaks(data, dim=-1, hmin=None, dmin=None, issort=True, returns=['pos', 'value'])

find peaks in data

Parameters:

  • data (Tensor) – the data tensor (N x S1 x S2 x … x SD)

  • dim (int or list, optional) – the number of dimensions should be equal to D, by default -1

  • hmin (float or None, optional) – the minimum height of peak, by default None

  • dmin (int, float or None, optional) – the minimum distance between two nearby peaks, by default None

  • issort (bool, optional) – sort peaks according to peak’s values before remove the peaks that does not satisfy the minimum distance constraint, by default True

  • returns (list, optional) – the variables to be returned, by default [‘pos’, ‘value’]

Examples

x = th.zeros(100, )
x[10] = 1.
x[30] = 1.2
x[32] = 0.9
x[34] = 1.1
x[90] = 0.3

print(findpeaks(x, dim=0, hmin=0.5, dmin=1))
print(findpeaks(x, dim=0, hmin=0.3, dmin=3))

x = th.zeros(60, 70, 80)
x[1, 20, 3] = 1.
x[2, 3, 20] = 0.5
x[2, 5, 20] = 1.3
x[2, 8, 20] = 0.3
print(findpeaks(x, dim=[0, 1, 2], hmin=0.5, dmin=1))
print(findpeaks(x, dim=[0, 1, 2], hmin=0.3, dmin=3))

# outputs:
[tensor([30, 34, 10, 32]), tensor([1.2000, 1.1000, 1.0000, 0.9000])]
[tensor([30, 34, 10, 90]), tensor([1.2000, 1.1000, 1.0000, 0.3000])]
[tensor([[ 2,  5, 20],
        [ 1, 20,  3],
        [ 2,  3, 20]]), tensor([1.3000, 1.0000, 0.5000])]
[tensor([[ 2,  5, 20],
        [ 1, 20,  3],
        [ 2,  8, 20]]), tensor([1.3000, 1.0000, 0.3000])]
torchbox.dsp.find_peaks.localmax1d(data, win=3, thresh=None, omode='sub')

find local maximum points

Pytorch Argrelmax (or C++) function

Parameters:

  • data (list, ndarray or Tensor) – the input data (L or Sbatch x L)

  • win (int, optional) – the local window size, by default 3

  • thresh (list, ndarray, Tensor or None, optional) – the threshhold, by default None

  • omode (str, optional) – not used argument since index and subscript are the same.

Examples

x = th.zeros(100, )
x[10] = 1.
x[30] = 1.2
x[31] = 0.9
x[80] = 1.
x[90] = 0.3

print(localmax1d(x, win=3, thresh=None))
print(localmax1d(x, win=2, thresh=None))
print(localmax1d(x, win=5))
print(localmax1d(x, win=5, thresh=0.8))

x = th.stack((x, x), dim=0)
print(localmax1d(x, win=3, thresh=None))
print(localmax1d(x, win=2, thresh=None))
print(localmax1d(x, win=5))
print(localmax1d(x, win=5, thresh=0.8))

# outputs
tensor([10, 30, 80, 90])
tensor([10, 30, 80, 90])
tensor([10, 30, 80, 90])
tensor([10, 30, 80])
[tensor([10, 30, 80, 90]), tensor([10, 30, 80, 90])]
[tensor([10, 30, 80, 90]), tensor([10, 30, 80, 90])]
[tensor([10, 30, 80, 90]), tensor([10, 30, 80, 90])]
[tensor([10, 30, 80]), tensor([10, 30, 80])]
torchbox.dsp.find_peaks.localmax2d(data, win=3, thresh=None, omode='sub')

find local maximum points

Pytorch Argrelmax (or C++) function

Parameters:

  • data (list, ndarray or Tensor) – the input data (H x W or Sbatch x H x W)

  • win (int, optional) – the local window size, by default 3

  • thresh (list, ndarray, Tensor or None, optional) – the threshhold, by default None

  • omode (str, optional) – output mode, 'ind' for indexes, 'sub' for subscription (default)

Examples

x = th.zeros((100, 100))
x[50, 30] = 1.
x[20, 80] = 0.1
print(localmax2d(x, win=3, thresh=0.8))

# outputs
tensor([[50, 30]])
torchbox.dsp.find_peaks.localmax3d(data, win=3, thresh=None, omode='sub')

find local maximum points

Pytorch Argrelmax (or C++) function

Parameters:

  • data (list, ndarray or Tensor) – the input data

  • win (int, optional) – the local window size, by default 3

  • thresh (list, ndarray, Tensor or None, optional) – the threshhold, by default None

  • omode (str, optional) – output mode, 'ind' for indexes, 'sub' for subscription (default)

Examples

x = th.zeros(60, 70, 80)
x[1, 20, 3] = 1.
x[2, 2, 20] = 0.3
print(localmax3d(x, win=3, thresh=None))

# outputs
tensor([[ 1, 20,  3],
        [ 2,  2, 20]])

torchbox.dsp.function_base module

torchbox.dsp.function_base.unwrap(x, discont=3.141592653589793, axis=-1, imp=None)

Unwrap by changing deltas between values to \(2\pi\) complement.

Unwrap radian phase x by changing absolute jumps greater than discont to their \(2\pi\) complement along the given axis.

Parameters:

  • x (Tensor or ndarray) – The input.

  • discont (float, optional) – Maximum discontinuity between values, default is \(\pi\).

  • axis (int, optional) – Axis along which unwrap will operate, default is the last axis.

  • imp (str, optional) – The implenmentation way, 'numpy' –> numpy, None or 'torch' –> torch (default)

Returns:

The unwrapped.

Return type:

Tensor or ndarray

Examples

x_np = np.array([3.14, -3.12, 3.12, 3.13, -3.11])
y_np = unwrap(x_np)
print(y_np, y_np.shape, type(y_np))
x_th = th.Tensor(x_np)
y_th = unwrap(x_th)
print(y_th, y_th.shape, type(y_th))

print("------------------------")
x_th = th.tensor([3.14, -3.12, 3.12, 3.13, -3.11])
x_th = th.cat((th.flip(x_th, dims=[0]), x_th), axis=0)
print(x_th)
y_th = unwrap2(x_th)
print(y_th, y_th.shape, type(y_th))

print("------------------------")
x_np = np.array([3.14, -3.12, 3.12, 3.13, -3.11])
x_th = th.Tensor(x_np)
y_th = unwrap(x_th, imp='numpy')
print(y_th, y_th.shape, type(y_th))

y_th = unwrap(x_th, imp=None)
print(y_th, y_th.shape, type(y_th))

# output

tensor([3.1400, 3.1632, 3.1200, 3.1300, 3.1732], dtype=torch.float64) torch.Size([5]) <class 'torch.Tensor'>
tensor([3.1400, 3.1632, 3.1200, 3.1300, 3.1732]) torch.Size([5]) <class 'torch.Tensor'>
------------------------
tensor([-3.1100,  3.1300,  3.1200, -3.1200,  3.1400,  3.1400, -3.1200,  3.1200,
        3.1300, -3.1100])
tensor([3.1732, 3.1300, 3.1200, 3.1632, 3.1400, 3.1400, 3.1632, 3.1200, 3.1300,
        3.1732]) torch.Size([10]) <class 'torch.Tensor'>
------------------------
tensor([3.1400, 3.1632, 3.1200, 3.1300, 3.1732]) torch.Size([5]) <class 'torch.Tensor'>
tensor([3.1400, 3.1632, 3.1200, 3.1300, 3.1732]) torch.Size([5]) <class 'torch.Tensor'>
torchbox.dsp.function_base.unwrap2(x, discont=3.141592653589793, axis=-1)

Unwrap by changing deltas between values to \(2\pi\) complement.

Unwrap radian phase x by changing absolute jumps greater than discont to their \(2\pi\) complement along the given axis. The elements are divided into 2 parts (with equal length) along the given axis. The first part is unwrapped in inverse order, while the second part is unwrapped in normal order.

Parameters:

  • x (Tensor) – The input.

  • discont (float, optional) – Maximum discontinuity between values, default is \(\pi\).

  • axis (int, optional) – Axis along which unwrap will operate, default is the last axis.

Returns:

  • Tensor – The unwrapped.

  • see also unwrap()

torchbox.dsp.interpolation module

torchbox.dsp.interpolation.interpolate(input, size=None, scale_factor=None, mode='nearest', align_corners=None, recompute_scale_factor=None)

Down/up samples the input to either the given size or the given scale_factor

The algorithm used for interpolation is determined by mode.

Currently temporal, spatial and volumetric sampling are supported, i.e. expected inputs are 3-D, 4-D or 5-D in shape.

The input dimensions are interpreted in the form: mini-batch x channels x [optional depth] x [optional height] x width.

The modes available for resizing are: nearest, linear (3D-only), bilinear, bicubic (4D-only), trilinear (5D-only), area

Parameters:

  • input (Tensor) – the input tensor

  • size (int or Tuple[int] or Tuple[int, int] or Tuple[int, int, int]) – output spatial size.

  • scale_factor (float or Tuple[float]) – multiplier for spatial size. Has to match input size if it is a tuple.

  • mode (str) – algorithm used for upsampling: 'nearest' | 'linear' | 'bilinear' | 'bicubic' | 'trilinear' | 'area'. Default: 'nearest'

  • align_corners (bool, optional) – Geometrically, we consider the pixels of the input and output as squares rather than points. If set to True, the input and output tensors are aligned by the center points of their corner pixels, preserving the values at the corner pixels. If set to False, the input and output tensors are aligned by the corner points of their corner pixels, and the interpolation uses edge value padding for out-of-boundary values, making this operation independent of input size when scale_factor is kept the same. This only has an effect when mode is 'linear', 'bilinear', 'bicubic' or 'trilinear'. Default: False

  • recompute_scale_factor (bool, optional) – recompute the scale_factor for use in the interpolation calculation. When scale_factor is passed as a parameter, it is used to compute the output_size. If recompute_scale_factor is `False or not specified, the passed-in scale_factor will be used in the interpolation computation. Otherwise, a new scale_factor will be computed based on the output and input sizes for use in the interpolation computation (i.e. the computation will be identical to if the computed output_size were passed-in explicitly). Note that when scale_factor is floating-point, the recomputed scale_factor may differ from the one passed in due to rounding and precision issues.

Note

With mode='bicubic', it’s possible to cause overshoot, in other words it can produce negative values or values greater than 255 for images. Explicitly call result.clamp(min=0, max=255) if you want to reduce the overshoot when displaying the image.

Warning

With align_corners = True, the linearly interpolating modes (linear, bilinear, and trilinear) don’t proportionally align the output and input pixels, and thus the output values can depend on the input size. This was the default behavior for these modes up to version 0.3.1. Since then, the default behavior is align_corners = False. See Upsample for concrete examples on how this affects the outputs.

Warning

When scale_factor is specified, if recompute_scale_factor=True, scale_factor is used to compute the output_size which will then be used to infer new scales for the interpolation. The default behavior for recompute_scale_factor changed to False in 1.6.0, and scale_factor is used in the interpolation calculation.

Note

When using the CUDA backend, this operation may induce nondeterministic behaviour in its backward pass that is not easily switched off. Please see the notes on /notes/randomness for background.

torchbox.dsp.interpolation.interpolatec(input, size=None, scale_factor=None, mode='nearest', align_corners=None, recompute_scale_factor=None)

Down/up samples the input to either the given size or the given scale_factor

The algorithm used for complex valued interpolation is determined by mode.

Currently temporal, spatial and volumetric sampling are supported, i.e. expected inputs are 3-D, 4-D or 5-D in shape.

The input dimensions are interpreted in the form: mini-batch x [optional channels] x [optional height] x width x 2.

The modes available for resizing are: nearest, linear (3D-only), bilinear, bicubic (4D-only), trilinear (5D-only), area

Parameters:

  • input (Tensor) – the input tensor

  • size (int or Tuple[int] or Tuple[int, int] or Tuple[int, int, int]) – output spatial size.

  • scale_factor (float or Tuple[float]) – multiplier for spatial size. Has to match input size if it is a tuple.

  • mode (str) – algorithm used for upsampling: 'nearest' | 'linear' | 'bilinear' | 'bicubic' | 'trilinear' | 'area'. Default: 'nearest'

  • align_corners (bool, optional) – Geometrically, we consider the pixels of the input and output as squares rather than points. If set to True, the input and output tensors are aligned by the center points of their corner pixels, preserving the values at the corner pixels. If set to False, the input and output tensors are aligned by the corner points of their corner pixels, and the interpolation uses edge value padding for out-of-boundary values, making this operation independent of input size when scale_factor is kept the same. This only has an effect when mode is 'linear', 'bilinear', 'bicubic' or 'trilinear'. Default: False

  • recompute_scale_factor (bool, optional) – recompute the scale_factor for use in the interpolation calculation. When scale_factor is passed as a parameter, it is used to compute the output_size. If recompute_scale_factor is `False or not specified, the passed-in scale_factor will be used in the interpolation computation. Otherwise, a new scale_factor will be computed based on the output and input sizes for use in the interpolation computation (i.e. the computation will be identical to if the computed output_size were passed-in explicitly). Note that when scale_factor is floating-point, the recomputed scale_factor may differ from the one passed in due to rounding and precision issues.

Note

With mode='bicubic', it’s possible to cause overshoot, in other words it can produce negative values or values greater than 255 for images. Explicitly call result.clamp(min=0, max=255) if you want to reduce the overshoot when displaying the image.

Warning

With align_corners = True, the linearly interpolating modes (linear, bilinear, and trilinear) don’t proportionally align the output and input pixels, and thus the output values can depend on the input size. This was the default behavior for these modes up to version 0.3.1. Since then, the default behavior is align_corners = False. See Upsample for concrete examples on how this affects the outputs.

Warning

When scale_factor is specified, if recompute_scale_factor=True, scale_factor is used to compute the output_size which will then be used to infer new scales for the interpolation. The default behavior for recompute_scale_factor changed to False in 1.6.0, and scale_factor is used in the interpolation calculation.

Note

When using the CUDA backend, this operation may induce nondeterministic behaviour in its backward pass that is not easily switched off. Please see the notes on /notes/randomness for background.

torchbox.dsp.kernels module

torchbox.dsp.normalsignals module

torchbox.dsp.normalsignals.chirp(t, fc, Kr, fm=0, pm=0, fmdir=-1, pmdir=-1, phi0=0, g=1)

create a chirp signal

\[s_{\rm Tx}(t)={\rm exp}\left\{j2\pi((f_c+f_m)t+{\beta /2}t^2)+p_m + \varphi_0\right\} \]
Parameters:

  • t (tensor) – the time tensor (s)

  • fc (float) – carrier frequency (Hz)

  • Kr (float) – chirp rate (Hz/s)

  • fm (float or tensor, optional) – modulated frequency, by default 0

  • pm (float or tensor, optional) – modulated phase, by default 0

  • fmdir (int, optional) – frequency modulation direction, 1 or -1, by default -1

  • pmdir (int, optional) – phase modulation direction, 1 or -1, , by default -1

  • phi0 (float, optional) – the initial phase, by default 0

  • g (float or tensor, optional) – effective gain/rcs/amplitude, by default 1

Returns:

chirp signal

Return type:

tensor

Examples

Tc = 10e-6
Fs = 100e6
B = 1e9
Kr = B / Tc
fc = 77e9
R = 100.

t = th.arange(0, Tc, 1./Fs)
st = chirp(t, fc, Kr)
sr = chirp(t-R/tb.C, fc, Kr)

sif = dechirp(sr, st)
y = tb.fft(sif).abs()

plt = tb.plot([[st.real, st.imag, st.abs()], [sr.real, sr.imag, sr.abs()], [sif.real, sif.imag, sif.abs()], [y]], Xs=[[t, t, t], [t, t, t], [t, t, t], [None]], grids=True, xlabels=['Times(s)', 'Times(s)', 'Times(s)', 'Frequency(Hz)'], legends=[['I', 'Q', 'A'], ['I', 'Q', 'A'], ['I', 'Q', 'A'], ['A']], titles=['Transmitted', 'Received', 'Dechirped', 'FFT of dechirped'])
plt.show()
torchbox.dsp.normalsignals.dechirp(srcv, sref, mod='+')

dechirp signal

Parameters:

  • srcv (tensor) – received signal

  • sref (tensor) – referenced signal

  • mod (str, optional) – dechirp mode, '+' means the term \(j2\pi f_c \tau_{k}\) in dechirped signal is positive otherwise, negative, by default ‘+’

Returns:

  • tensor – dechirped signal

torchbox.dsp.normalsignals.rect(t)

create rectangle signal

\[{\rm rect}(x) = {1, {\rm if} |x|<= 0.5; 0, {\rm otherwise}} \]
Parameters:

t (tensor) – time tensor

Returns:

rectangle signal

Return type:

tensor

Examples

import torchbox as tb

Ts = 3
Fs = 100
Ns = int(Ts * Fs)
t = th.linspace(-Ts / 2., Ts / 2., Ns)

x = tb.rect(t)

plt = tb.plot([[x]], Xs=[[t]], grids=True, xlabels=['Times(s)'])
plt.show()

torchbox.dsp.polynomialfit module

torchbox.dsp.polynomialfit.polyfit(x, y, deg=1, C=1)

Least squares polynomial fit.

We fit the data using a polynomial function of the form

\[y(x, {\mathbf w})=w_{0}+w_{1} x+w_{2} x^{2}+, \cdots,+w_{M} x^{M}=\sum_{j=0}^{M} w_{j} x^{j} \]

where \(M\) is the order of the polynomial, and \(x^{j}\) denotes \(x\) raised to the power of \(j\), The polynomial coefficients \(w_{0}, w_{1}, \cdots \cdot w_{M}\) comprise the vector \(\mathbf{w}=\left(w_{0}, w_{1}, \cdots \cdot w_{M}\right)^{\mathrm{T}}\).

This can be done by minimizing an error function

..math::

E(mathbf{w})=frac{1}{2} sum_{n=1}^{N}left{yleft(x_{n}, mathbf{w}right)-t_{n}right}^{2} + C |{mathbf w}|_2^2

the solution is

\[\mathbf{w}=\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \mathbf{t} \]

see https://iridescent.blog.csdn.net/article/details/39554293

Parameters:

  • x (torch 1d tensor) – x-coordinates of the N sample points \((x[i], y[i])\)

  • y (torch 1d tensor) – y-coordinates of the N sample points \((x[i], y[i])\)

  • deg (int or tuple or list, optional) – degree (\(M\)) of the fitting polynomial, deg[0] is the minimum degree, deg[1] is the maximum degree, if deg is an integer, the minimum degree is 0 , the maximum degree is deg (the default is 1)

  • C (float, optional) – the balance factor of weight regularization and fitting error.

Returns:

  • w (torch 1d tensor) – The polynomial coefficients \(w_{0}, w_{1}, \cdots \cdot w_{M}\).

  • see also polyval(), rmlinear().

Examples

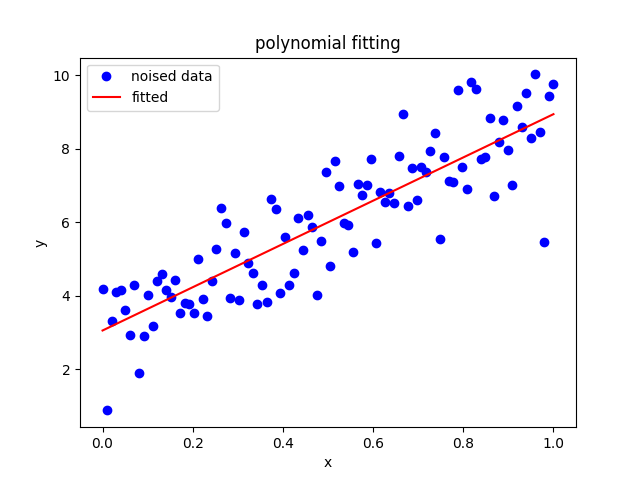
_images/PolynomialFitting.png

The results shown in the above figure can be obtained by the following codes.

import matplotlib.pyplot as plt

Ns, k, b = 100, 6.2, 3.0
x = th.linspace(0, 1, Ns)
y = x * k + b + th.randn(Ns)
# x, y = x.to('cuda:1'), y.to('cuda:1')

w = polyfit(x, y, deg=1)
print(w, w.shape)
w = polyfit(x, y, deg=1, C=5)
print(w)
yy = polyval(w, x)
print(yy)

print(th.sum(th.abs(y - yy)))

plt.figure()
plt.plot(x, y, 'ob')
plt.plot(x, yy, '-r')
plt.xlabel('x')
plt.ylabel('y')
plt.title('polynomial fitting')
plt.legend(['noised data', 'fitted'])
plt.show()
torchbox.dsp.polynomialfit.polyval(w, x, deg=None)

Evaluate a polynomial at specific values.

We fit the data using a polynomial function of the form

\[y(x, \mathbf{w})=w_{0}+w_{1} x+w_{2} x^{2}+, \cdots,+w_{M} x^{M}=\sum_{j=0}^{M} w_{j} x^{j} \]
Parameters:

  • w (torch 1d tensor) – the polynomial coefficients \(w_{0}, w_{1}, \cdots \cdot w_{M}\) with shape M-N, where N is the number of coefficients, and M is the degree.

  • x (torch 1d tensor) – x-coordinates of the N sample points \((x[i], y[i])\)

  • deg (int or tuple or list or None, optional) – degree (\(M\)) of the fitting polynomial, deg[0] is the minimum degree, deg[1] is the maximum degree; if deg is an integer, the minimum degree is 0, the maximum degree is deg; if deg is None, the minimum degree is 0 the maximum degree is ``w.shape[1] - 1``(the default is None)

Returns:

  • y (torch 1d tensor) – y-coordinates of the N sample points \((x[i], y[i])\)

  • see also polyfit(), rmlinear().

torchbox.dsp.polynomialfit.rmlinear(x, y, deg=2, C=1)

Remove linear trend

After the data is fitted by

\[y(x, \mathbf{w})=w_{0}+w_{1} x+w_{2} x^{2}+, \cdots,+w_{M} x^{M}=\sum_{j=0}^{M} w_{j} x^{j} \]

the constant and linear trend can be removed by setting \(w_{0}=w_{1}=0\), or simply by fitting the data with 2 to \(M\) order polynominal.

Parameters:

  • x (torch 1d tensor) – x-coordinates of the N sample points \((x[i], y[i])\)

  • y (torch 1d tensor) – y-coordinates of the N sample points \((x[i], y[i])\)

  • deg (int, optional) – degree (\(M\)) of the fitting polynomial (the default is 1)

  • C (float, optional) – the balance factor of weight regularization and fitting error.

Returns:

  • y (torch 1d tensor) – y-coordinates of the N sample points \((x[i], y[i])\), linear trend is removed.

  • see also polyval(), polyfit().

torchbox.dsp.window_function module

torchbox.dsp.window_function.window(n, wtype=None, isperiodic=True, dtype=None, device=None, requires_grad=False)

Generates window

Parameters:

  • n (int) – The length of the window.

  • wtype (str or None, optional) – The window type: - 'rectangle' for rectangle window - 'bartlett' for bartlett window - 'blackman' for blackman window - 'hamming x y' for hamming window with \(\alpha=x, \beta=y\), default is 0.54, 0.46. - 'hanning' for hanning window - 'kaiser x' for kaiser window with \(\beta=x\), default is 12.

  • isperiodic (bool, optional) – If True (default), returns a window to be used as periodic function. If False, return a symmetric window.

  • dtype (None, optional) – The desired data type of returned tensor.

  • device (None, optional) – The desired device of returned tensor.

  • requires_grad (bool, optional) – If autograd should record operations on the returned tensor. Default: False.

Returns:

A 1-D tensor of size (n,) containing the window

Return type:

tensor

torchbox.dsp.window_function.windowing(x, w, axis=None)

Performs windowing operation in the specified axis.

Parameters:

  • x (Tensor) – The input tensor.

  • w (Tensor) – A 1-d window tensor.

  • axis (int or None, optional) – The axis.

Returns:

The windowed data.

Return type:

tensor

Module contents