pyaibox.evaluation package

Submodules

pyaibox.evaluation.classification module

pyaibox.evaluation.classification.accuracy(P, T, axis=None)

computes the accuracy

\[A = \frac{\sum(P==T)}{N} \]

where \(N\) is the number of samples.

Parameters

  • P (list or array) – predicted label (categorical or one-hot)

  • T (list or array) – target label (categorical or one-hot)

  • axis (int, optional) – the one-hot encoding axis, by default None, which means P and T are categorical.

Returns

the accuracy

Return type

float

Raises

  • ValueError – P and T should have the same shape!

  • ValueError – You should specify the one-hot encoding axis when P and T are in one-hot formation!

Examples

import pyaibox as pb

T = np.array([1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 5])
P = np.array([1, 2, 3, 4, 1, 6, 3, 2, 1, 4, 5, 6, 1, 2, 1, 4, 5, 6, 1, 5])

print(pb.accuracy(P, T))

#---output
0.8
pyaibox.evaluation.classification.categorical2onehot(X, nclass=None)

converts categorical to onehot

Parameters

  • X (list or array) – the categorical list or array

  • nclass (int, optional) – the number of classes, by default None (auto detected)

Returns

the one-hot matrix

Return type

array

pyaibox.evaluation.classification.confusion(P, T, axis=None, cmpmode='...')

computes the confusion matrix

Parameters

  • P (list or array) – predicted label (categorical or one-hot)

  • T (list or array) – target label (categorical or one-hot)

  • axis (int, optional) – the one-hot encoding axis, by default None, which means P and T are categorical.

  • cmpmode (str, optional) – '...' for one-by one mode, '@' for multiplication mode (\(P^TT\)), by default ‘…’

Returns

the confusion matrix

Return type

array

Raises

  • ValueError – P and T should have the same shape!

  • ValueError – You should specify the one-hot encoding axis when P and T are in one-hot formation!

Examples

import pyaibox as pb

T = np.array([1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 5])
P = np.array([1, 2, 3, 4, 1, 6, 3, 2, 1, 4, 5, 6, 1, 2, 1, 4, 5, 6, 1, 5])

C = pb.confusion(P, T, cmpmode='...')
print(C)
C = pb.confusion(P, T, cmpmode='@')
print(C)

#---output
[[3. 0. 2. 0. 1. 0.]
[0. 3. 0. 0. 0. 0.]
[1. 0. 1. 0. 0. 0.]
[0. 0. 0. 3. 0. 0.]
[0. 0. 0. 0. 3. 0.]
[0. 0. 0. 0. 0. 3.]]
[[3. 0. 2. 0. 1. 0.]
[0. 3. 0. 0. 0. 0.]
[1. 0. 1. 0. 0. 0.]
[0. 0. 0. 3. 0. 0.]
[0. 0. 0. 0. 3. 0.]
[0. 0. 0. 0. 0. 3.]]
pyaibox.evaluation.classification.kappa(C)

computes kappa

\[K = \frac{p_o - p_e}{1 - p_e} \]

where \(p_o\) and \(p_e\) can be obtained by

\[p_o = \frac{\sum_iC_{ii}}{\sum_i\sum_jC_{ij}} \]
\[p_e = \frac{\sum_j\left(\sum_iC_{ij}\sum_iC_{ji}\right)}{\sum_i\sum_jC_{ij}} \]
Parameters

C (array) – The confusion matrix

Returns

The kappa value.

Return type

float

Examples

import pyaibox as pb

T = np.array([1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 5])
P = np.array([1, 2, 3, 4, 1, 6, 3, 2, 1, 4, 5, 6, 1, 2, 1, 4, 5, 6, 1, 5])

C = pb.confusion(P, T, cmpmode='...')
print(pb.kappa(C))
print(pb.kappa(C.T))

#---output
0.7583081570996979
0.7583081570996979
pyaibox.evaluation.classification.onehot2categorical(X, axis=-1, offset=0)

converts onehot to categorical

Parameters

  • X (list or array) – the one-hot array

  • axis (int, optional) – the axis for one-hot encoding, by default -1

  • offset (int, optional) – category label head, by default 0

Returns

the category label

Return type

array

pyaibox.evaluation.classification.plot_confusion(C, cmap=None, xlabel='Target', ylabel='Predicted', title='Confusion matrix', **kwargs)

plots confusion matrix.

plots confusion matrix.

Parameters

  • C (array) – The confusion matrix

  • cmap (None or str, optional) – The colormap, by default None, which means our default configuration (green-coral)

  • xlabel (str, optional) – The label string of axis-x, by default ‘Target’

  • ylabel (str, optional) – The label string of axis-y, by default ‘Predicted’

  • title (str, optional) – The title string, by default ‘Confusion matrix’

  • kwargs –

    linespacingfloat

    The line spacing of text, by default 0.15

    numftddict

    The font dict of integer value, by default dict(fontsize=12, color='black', family='Times New Roman', weight='bold', style='normal')

    pctftddict

    The font dict of percent value, by default dict(fontsize=12, color='black', family='Times New Roman', weight='light', style='normal')

    pctfmtdict

    the format of percent value, such as '%.xf' means formating with two decimal places, by default '%.1f'

Returns

pyplot handle

Return type

pyplot

Example

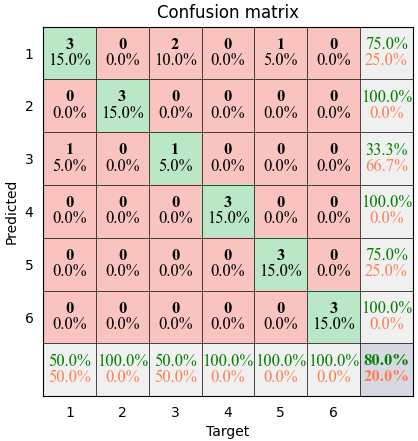
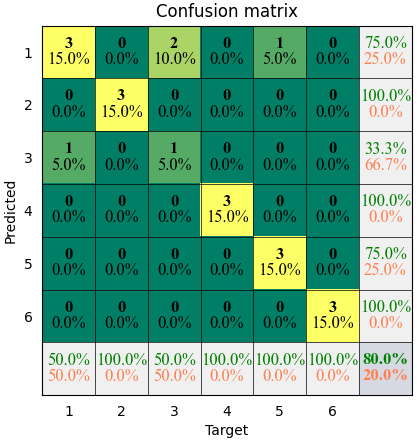
_images/ConfusionMatrixDefault.png _images/ConfusionMatrixSummer.png

The results shown in the above figure can be obtained by the following codes.

import pyaibox as pb

T = np.array([1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 5])
P = np.array([1, 2, 3, 4, 1, 6, 3, 2, 1, 4, 5, 6, 1, 2, 1, 4, 5, 6, 1, 5])

C = pb.confusion(P, T, cmpmode='@')

plt = pb.plot_confusion(C, cmap=None)
plt = pb.plot_confusion(C, cmap='summer')
plt.show()

pyaibox.evaluation.contrast module

pyaibox.evaluation.contrast.contrast(X, caxis=None, axis=None, mode='way1', reduction='mean')

Compute contrast of an complex image

'way1' is defined as follows, see [1]:

\[C = \frac{\sqrt{{\rm E}\left(|I|^2 - {\rm E}(|I|^2)\right)^2}}{{\rm E}(|I|^2)} \]

'way2' is defined as follows, see [2]:

\[C = \frac{{\rm E}(|I|^2)}{\left({\rm E}(|I|)\right)^2} \]

[1] Efficient Nonparametric ISAR Autofocus Algorithm Based on Contrast Maximization and Newton [2] section 13.4.1 in “Ian G. Cumming’s SAR book”

Parameters

  • X (numpy ndarray) – The image array.

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing contrast. The default is None, which means all.

  • mode (str, optional) – 'way1' or 'way2'

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

C – The contrast value of input.

Return type

scalar or numpy array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)

# real
C1 = contrast(X, caxis=None, axis=(-2, -1), mode='way1', reduction=None)
C2 = contrast(X, caxis=None, axis=(-2, -1), mode='way1', reduction='sum')
C3 = contrast(X, caxis=None, axis=(-2, -1), mode='way1', reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = contrast(X, caxis=1, axis=(-2, -1), mode='way1', reduction=None)
C2 = contrast(X, caxis=1, axis=(-2, -1), mode='way1', reduction='sum')
C3 = contrast(X, caxis=1, axis=(-2, -1), mode='way1', reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
C1 = contrast(X, caxis=None, axis=(-2, -1), mode='way1', reduction=None)
C2 = contrast(X, caxis=None, axis=(-2, -1), mode='way1', reduction='sum')
C3 = contrast(X, caxis=None, axis=(-2, -1), mode='way1', reduction='mean')
print(C1, C2, C3)

# ---output
[[1.07323512 1.39704055]
[0.96033633 1.35878254]
[1.57174342 1.42973702]
[1.37236497 1.2351262 ]
[1.06519696 1.4606771 ]] 12.924240207170865 1.2924240207170865
[0.86507341 1.03834259 1.00448054 0.89381925 1.20616657] 5.007882367336851 1.0015764734673702
[0.86507341 1.03834259 1.00448054 0.89381925 1.20616657] 5.007882367336851 1.0015764734673702

pyaibox.evaluation.detection_voc module

pyaibox.evaluation.detection_voc.bbox_iou(bbox_a, bbox_b)

Calculate the Intersection of Unions (IoUs) between bounding boxes.

IoU is calculated as a ratio of area of the intersection and area of the union. This function accepts both numpy.ndarray and cupy.ndarray as inputs. Please note that both bbox_a and bbox_b need to be same type. The output is same type as the type of the inputs.

Parameters

  • bbox_a (array) – An array whose shape is \((N, 4)\). \(N\) is the number of bounding boxes. The dtype should be numpy.float32.

  • bbox_b (array) – An array similar to bbox_a, whose shape is \((K, 4)\). The dtype should be numpy.float32.

Returns

array An array whose shape is \((N, K)\). An element at index \((n, k)\) contains IoUs between \(n\) th bounding box in bbox_a and \(k\) th bounding box in bbox_b.

pyaibox.evaluation.detection_voc.calc_detection_voc_ap(prec, rec, use_07_metric=False)

Calculate average precisions based on evaluation code of PASCAL VOC.

This function calculates average precisions from given precisions and recalls. The code is based on the evaluation code used in PASCAL VOC Challenge.

Parameters

  • prec (list of numpy.array) – A list of arrays. prec[l] indicates precision for class \(l\). If prec[l] is None, this function returns numpy.nan for class \(l\).

  • rec (list of numpy.array) – A list of arrays. rec[l] indicates recall for class \(l\). If rec[l] is None, this function returns numpy.nan for class \(l\).

  • use_07_metric (bool) – Whether to use PASCAL VOC 2007 evaluation metric for calculating average precision. The default value is False.

Returns

This function returns an array of average precisions. The \(l\)-th value corresponds to the average precision for class \(l\). If prec[l] or rec[l] is None, the corresponding value is set to numpy.nan.

Return type

ndarray

pyaibox.evaluation.detection_voc.calc_detection_voc_prec_rec(pred_bboxes, pred_labels, pred_scores, gt_bboxes, gt_labels, gt_difficults=None, iou_thresh=0.5)

Calculate precision and recall based on evaluation code of PASCAL VOC.

This function calculates precision and recall of predicted bounding boxes obtained from a dataset which has \(N\) images. The code is based on the evaluation code used in PASCAL VOC Challenge.

Parameters

  • pred_bboxes (iterable of numpy.ndarray) – An iterable of \(N\) sets of bounding boxes. Its index corresponds to an index for the base dataset. Each element of pred_bboxes is a set of coordinates of bounding boxes. This is an array whose shape is \((R, 4)\), where \(R\) corresponds to the number of bounding boxes, which may vary among boxes. The second axis corresponds to \(y_{min}, x_{min}, y_{max}, x_{max}\) of a bounding box.

  • pred_labels (iterable of numpy.ndarray) – An iterable of labels. Similar to pred_bboxes, its index corresponds to an index for the base dataset. Its length is \(N\).

  • pred_scores (iterable of numpy.ndarray) – An iterable of confidence scores for predicted bounding boxes. Similar to pred_bboxes, its index corresponds to an index for the base dataset. Its length is \(N\).

  • gt_bboxes (iterable of numpy.ndarray) – An iterable of ground truth bounding boxes whose length is \(N\). An element of gt_bboxes is a bounding box whose shape is \((R, 4)\). Note that the number of bounding boxes in each image does not need to be same as the number of corresponding predicted boxes.

  • gt_labels (iterable of numpy.ndarray) – An iterable of ground truth labels which are organized similarly to gt_bboxes.

  • gt_difficults (iterable of numpy.ndarray) – An iterable of boolean arrays which is organized similarly to gt_bboxes. This tells whether the corresponding ground truth bounding box is difficult or not. By default, this is None. In that case, this function considers all bounding boxes to be not difficult.

  • iou_thresh (float) – A prediction is correct if its Intersection over Union with the ground truth is above this value..

Returns

This function returns two lists: prec and rec.

  • prec: A list of arrays. prec[l] is precision

    for class \(l\). If class \(l\) does not exist in either pred_labels or gt_labels, prec[l] is set to None.

  • rec: A list of arrays. rec[l] is recall

    for class \(l\). If class \(l\) that is not marked as difficult does not exist in gt_labels, rec[l] is set to None.

Return type

tuple of two lists

pyaibox.evaluation.detection_voc.eval_detection_voc(pred_bboxes, pred_labels, pred_scores, gt_bboxes, gt_labels, gt_difficults=None, iou_thresh=0.5, use_07_metric=False)

Calculate average precisions based on evaluation code of PASCAL VOC.

This function evaluates predicted bounding boxes obtained from a dataset which has \(N\) images by using average precision for each class. The code is based on the evaluation code used in PASCAL VOC Challenge.

Parameters

  • pred_bboxes (iterable of numpy.ndarray) – An iterable of \(N\) sets of bounding boxes. Its index corresponds to an index for the base dataset. Each element of pred_bboxes is a set of coordinates of bounding boxes. This is an array whose shape is \((R, 4)\), where \(R\) corresponds to the number of bounding boxes, which may vary among boxes. The second axis corresponds to \(y_{min}, x_{min}, y_{max}, x_{max}\) of a bounding box.

  • pred_labels (iterable of numpy.ndarray) – An iterable of labels. Similar to pred_bboxes, its index corresponds to an index for the base dataset. Its length is \(N\).

  • pred_scores (iterable of numpy.ndarray) – An iterable of confidence scores for predicted bounding boxes. Similar to pred_bboxes, its index corresponds to an index for the base dataset. Its length is \(N\).

  • gt_bboxes (iterable of numpy.ndarray) – An iterable of ground truth bounding boxes whose length is \(N\). An element of gt_bboxes is a bounding box whose shape is \((R, 4)\). Note that the number of bounding boxes in each image does not need to be same as the number of corresponding predicted boxes.

  • gt_labels (iterable of numpy.ndarray) – An iterable of ground truth labels which are organized similarly to gt_bboxes.

  • gt_difficults (iterable of numpy.ndarray) – An iterable of boolean arrays which is organized similarly to gt_bboxes. This tells whether the corresponding ground truth bounding box is difficult or not. By default, this is None. In that case, this function considers all bounding boxes to be not difficult.

  • iou_thresh (float) – A prediction is correct if its Intersection over Union with the ground truth is above this value.

  • use_07_metric (bool) – Whether to use PASCAL VOC 2007 evaluation metric for calculating average precision. The default value is False.

Returns

The keys, value-types and the description of the values are listed below.

  • ap (ndarray): An array of average precisions.

    The \(l\)-th value corresponds to the average precision for class \(l\). If class \(l\) does not exist in either pred_labels or gt_labels, the corresponding value is set to numpy.nan.

  • map (float): The average of Average Precisions over classes.

Return type

dict

pyaibox.evaluation.entropy module

pyaibox.evaluation.entropy.entropy(X, caxis=None, axis=None, mode='shannon', reduction='mean')

compute the entropy of the inputs

\[{\rm ENT} = -\sum_{n=0}^N p_i{\rm log}_2 p_n \]

where \(N\) is the number of pixels, \(p_n=\frac{|X_n|^2}{\sum_{n=0}^N|X_n|^2}\).

Parameters

  • X (numpy array) – The complex or real inputs, for complex inputs, both complex and real representations are surpported.

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing entropy. The default is None, which means all.

  • mode (str, optional) – The entropy mode: 'shannon' or 'natural' (the default is ‘shannon’)

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

S – The entropy of the inputs.

Return type

scalar or numpy array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)

# real
S1 = entropy(X, caxis=None, axis=(-2, -1), mode='shannon', reduction=None)
S2 = entropy(X, caxis=None, axis=(-2, -1), mode='shannon', reduction='sum')
S3 = entropy(X, caxis=None, axis=(-2, -1), mode='shannon', reduction='mean')
print(S1, S2, S3)

# complex in real format
S1 = entropy(X, caxis=1, axis=(-2, -1), mode='shannon', reduction=None)
S2 = entropy(X, caxis=1, axis=(-2, -1), mode='shannon', reduction='sum')
S3 = entropy(X, caxis=1, axis=(-2, -1), mode='shannon', reduction='mean')
print(S1, S2, S3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
S1 = entropy(X, caxis=None, axis=(-2, -1), mode='shannon', reduction=None)
S2 = entropy(X, caxis=None, axis=(-2, -1), mode='shannon', reduction='sum')
S3 = entropy(X, caxis=None, axis=(-2, -1), mode='shannon', reduction='mean')
print(S1, S2, S3)

# ---output
[[2.76482544 2.38657794]
[2.85232291 2.33204624]
[2.26890769 2.4308547 ]
[2.50283407 2.56037192]
[2.76608007 2.47020486]] 25.33502585795305 2.533502585795305
[3.03089227 2.84108823 2.93389666 3.00868855 2.8229912 ] 14.637556915006513 2.9275113830013026
[3.03089227 2.84108823 2.93389666 3.00868855 2.8229912 ] 14.637556915006513 2.9275113830013026

pyaibox.evaluation.error module

pyaibox.evaluation.error.ampphaerror(orig, reco)

compute amplitude phase error

compute amplitude phase error of two complex valued matrix

Parameters

  • orig (numpy array) – orignal

  • reco (numpy array) – reconstructed

Returns

  • amperror (float) – error of amplitude

  • phaerror (float) – error of phase

pyaibox.evaluation.error.mae(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the mean absoluted error

Both complex and real representation are supported.

\[{\rm MAE}({\bf X, Y}) = \frac{1}{N}\||{\bf X} - {\bf Y}|\| = \frac{1}{N}\sum_{i=1}^N |x_i - y_i| \]
Parameters

  • X (array) – original

  • Y (array) – reconstructed

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

mean absoluted error

Return type

scalar or array

Examples

norm = False
np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = mae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = mae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = mae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = mae(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = mae(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = mae(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = mae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = mae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = mae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# ---output
[[1.06029116 1.19884877]
[0.90117091 1.13552361]
[1.23422083 0.75743914]
[1.16127965 1.42169262]
[1.25090731 1.29134222]] 11.41271620974502 1.141271620974502
[1.71298566 1.50327364 1.53328572 2.11430946 2.01435599] 8.878210471231741 1.7756420942463482
[1.71298566 1.50327364 1.53328572 2.11430946 2.01435599] 8.878210471231741 1.7756420942463482
pyaibox.evaluation.error.mse(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the mean square error

Both complex and real representation are supported.

\[{\rm MSE}({\bf X, Y}) = \frac{1}{N}\|{\bf X} - {\bf Y}\|_2^2 = \frac{1}{N}\sum_{i=1}^N(|x_i - y_i|)^2 \]
Parameters

  • X (array) – reconstructed

  • Y (array) – target

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

mean square error

Return type

scalar or array

Examples

norm = False
np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = mse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = mse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = mse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = mse(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = mse(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = mse(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = mse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = mse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = mse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# ---output
[[1.57602573 2.32844311]
[1.07232374 2.36118382]
[2.1841515  0.79002805]
[2.43036295 3.18413899]
[2.31107373 2.73990485]] 20.977636476183186 2.0977636476183186
[3.90446884 3.43350757 2.97417955 5.61450194 5.05097858] 20.977636476183186 4.195527295236637
[3.90446884 3.43350757 2.97417955 5.61450194 5.05097858] 20.977636476183186 4.195527295236637
pyaibox.evaluation.error.nmae(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the normalized mean absoluted error

Both complex and real representation are supported.

\[{\rm NMAE}({\bf X, Y}) = \frac{\frac{1}{N}\||{\bf X} - {\bf Y}|\|}{\||{\bf Y}|\|} \]
Parameters

  • X (array) – original

  • Y (array) – reconstructed

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

mean absoluted error

Return type

scalar or array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = nmae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = nmae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = nmae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = nmae(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = nmae(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = nmae(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = nmae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = nmae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = nmae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)
pyaibox.evaluation.error.nmse(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the normalized mean square error

Both complex and real representation are supported.

\[{\rm NMSE}({\bf X, Y}) = \frac{\frac{1}{N}\|{\bf X} - {\bf Y}\|_2^2}{\|{\bf Y}\|_2^2}= \frac{\frac{1}{N}\sum_{i=1}^N(|x_i - y_i|)^2}{\sum_{i=1}^N(|y_i|)^2} \]
Parameters

  • X (array) – reconstructed

  • Y (array) – target

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

mean square error

Return type

scalar or array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = nmse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = nmse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = nmse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = nmse(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = nmse(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = nmse(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = nmse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = nmse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = nmse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)
pyaibox.evaluation.error.nsae(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the normalized sum absoluted error

Both complex and real representation are supported.

\[{\rm NSAE}({\bf X, Y}) = \frac{\||{\bf X} - {\bf Y}|\|}{\||{\bf Y}|\|} = \frac{\sum_{i=1}^N |x_i - y_i|}{\sum_{i=1}^N |y_i|} \]
Parameters

  • X (array) – original

  • Y (array) – reconstructed

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

sum absoluted error

Return type

scalar or array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = nsae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = nsae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = nsae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = nsae(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = nsae(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = nsae(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = nsae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = nsae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = nsae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)
pyaibox.evaluation.error.nsse(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the normalized sum square error

Both complex and real representation are supported.

\[{\rm NSSE}({\bf X, Y}) = \frac{\|{\bf X} - {\bf Y}\|_2^2}{\|{\bf Y}\|_2^2} = \frac{\sum_{i=1}^N(|x_i - y_i|)^2}{\sum_{i=1}^N(|y_i|)^2} \]
Parameters

  • X (array) – reconstructed

  • Y (array) – target

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

sum square error

Return type

scalar or array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = sse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = sse(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = sse(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = sse(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = sse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)
pyaibox.evaluation.error.sae(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the sum absoluted error

Both complex and real representation are supported.

\[{\rm SAE}({\bf X, Y}) = \||{\bf X} - {\bf Y}|\| = \sum_{i=1}^N |x_i - y_i| \]
Parameters

  • X (array) – original

  • Y (array) – reconstructed

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

sum absoluted error

Return type

scalar or array

Examples

norm = False
np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = sae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = sae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = sae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = sae(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = sae(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = sae(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = sae(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = sae(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = sae(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# ---output
[[12.72349388 14.3861852 ]
[10.81405096 13.62628335]
[14.81065     9.08926963]
[13.93535577 17.0603114 ]
[15.0108877  15.49610662]] 136.95259451694022 13.695259451694023
[20.55582795 18.03928365 18.39942858 25.37171356 24.17227192] 106.53852565478087 21.307705130956172
[20.55582795 18.03928365 18.39942858 25.37171356 24.17227192] 106.5385256547809 21.30770513095618
pyaibox.evaluation.error.sse(X, Y, caxis=None, axis=None, keepcaxis=False, reduction='mean')

computes the sum square error

Both complex and real representation are supported.

\[{\rm SSE}({\bf X, Y}) = \|{\bf X} - {\bf Y}\|_2^2 = \sum_{i=1}^N(|x_i - y_i|)^2 \]
Parameters

  • X (array) – reconstructed

  • Y (array) – target

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • keepcaxis (bool) – If True, the complex dimension will be keeped. Only works when X is complex-valued tensor but represents in real format. Default is False.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

sum square error

Return type

scalar or array

Examples

norm = False
np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)
Y = np.random.randn(5, 2, 3, 4)

# real
C1 = sse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = sse(X, Y, caxis=1, axis=(-2, -1), reduction=None)
C2 = sse(X, Y, caxis=1, axis=(-2, -1), reduction='sum')
C3 = sse(X, Y, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
Y = Y[:, 0, ...] + 1j * Y[:, 1, ...]
C1 = sse(X, Y, caxis=None, axis=(-2, -1), reduction=None)
C2 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='sum')
C3 = sse(X, Y, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# ---output
[[18.91230872 27.94131733]
[12.86788492 28.33420589]
[26.209818    9.48033663]
[29.16435541 38.20966786]
[27.73288477 32.87885818]] 251.73163771419823 25.173163771419823
[46.85362605 41.20209081 35.69015462 67.37402327 60.61174295] 251.73163771419823 50.346327542839646
[46.85362605 41.20209081 35.69015462 67.37402327 60.61174295] 251.73163771419823 50.346327542839646

pyaibox.evaluation.norm module

pyaibox.evaluation.norm.fnorm(X, caxis=None, axis=None, reduction='mean')

obtain the f-norm of a array

Both complex and real representation are supported.

\[{\rm fnorm}({\bf X}) = \|{\bf X}\|_2 = \left(\sum_{x_i\in {\bf X}}|x_i|^2\right)^{\frac{1}{2}} = \left(\sum_{x_i\in {\bf X}}(u_i^2 + v_i^2)\right)^{\frac{1}{2}} \]

where, \(u, v\) are the real and imaginary part of \(x\), respectively.

Parameters

  • X (array) – input

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

the inputs’s f-norm.

Return type

array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)

# real
C1 = fnorm(X, caxis=None, axis=(-2, -1), reduction=None)
C2 = fnorm(X, caxis=None, axis=(-2, -1), reduction='sum')
C3 = fnorm(X, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = fnorm(X, caxis=1, axis=(-2, -1), reduction=None)
C2 = fnorm(X, caxis=1, axis=(-2, -1), reduction='sum')
C3 = fnorm(X, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
C1 = fnorm(X, caxis=None, axis=(-2, -1), reduction=None)
C2 = fnorm(X, caxis=None, axis=(-2, -1), reduction='sum')
C3 = fnorm(X, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# ---output
---norm
[[3.18214671 3.28727232]
[3.52423801 3.45821738]
[3.07757733 3.23720035]
[2.45488229 3.98372024]
[2.23480914 3.73551246]] 32.1755762254205 3.21755762254205
[4.57517398 4.93756225 4.46664844 4.67936684 4.35297889] 23.011730410021634 4.602346082004327
[4.57517398 4.93756225 4.46664844 4.67936684 4.35297889] 23.011730410021634 4.602346082004327
pyaibox.evaluation.norm.pnorm(X, caxis=None, axis=None, p=2, reduction='mean')

obtain the p-norm of a array

Both complex and real representation are supported.

\[{\rm pnorm}({\bf X}) = \|{\bf X}\|_p = \left(\sum_{x_i\in {\bf X}}|x_i|^p\right)^{\frac{1}{p}} = \left(\sum_{x_i\in {\bf X}}\sqrt{u_i^2+v^2}^p\right)^{\frac{1}{p}} \]

where, \(u, v\) are the real and imaginary part of \(x\), respectively.

Parameters

  • X (array) – input

  • caxis (int or None) – If X is complex-valued, caxis is ignored. If X is real-valued and caxis is integer then X will be treated as complex-valued, in this case, caxis specifies the complex axis; otherwise (None), X will be treated as real-valued

  • axis (int or None) – The dimension axis (caxis is not included) for computing norm. The default is None, which means all.

  • p (int) – Specifies the power. The default is 2.

  • reduction (str, optional) – The operation in batch dim, None, 'mean' or 'sum' (the default is 'mean')

Returns

the inputs’s p-norm.

Return type

array

Examples

np.random.seed(2020)
X = np.random.randn(5, 2, 3, 4)

# real
C1 = pnorm(X, caxis=None, axis=(-2, -1), reduction=None)
C2 = pnorm(X, caxis=None, axis=(-2, -1), reduction='sum')
C3 = pnorm(X, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in real format
C1 = pnorm(X, caxis=1, axis=(-2, -1), reduction=None)
C2 = pnorm(X, caxis=1, axis=(-2, -1), reduction='sum')
C3 = pnorm(X, caxis=1, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# complex in complex format
X = X[:, 0, ...] + 1j * X[:, 1, ...]
C1 = pnorm(X, caxis=None, axis=(-2, -1), reduction=None)
C2 = pnorm(X, caxis=None, axis=(-2, -1), reduction='sum')
C3 = pnorm(X, caxis=None, axis=(-2, -1), reduction='mean')
print(C1, C2, C3)

# ---output
---pnorm
[[3.18214671 3.28727232]
[3.52423801 3.45821738]
[3.07757733 3.23720035]
[2.45488229 3.98372024]
[2.23480914 3.73551246]] 32.1755762254205 3.21755762254205
[4.57517398 4.93756225 4.46664844 4.67936684 4.35297889] 23.011730410021634 4.602346082004327
[4.57517398 4.93756225 4.46664844 4.67936684 4.35297889] 23.011730410021634 4.602346082004327

pyaibox.evaluation.snrs module

pyaibox.evaluation.snrs.psnr(P, G, vpeak=None, **kwargs)

Peak Signal-to-Noise Ratio

The Peak Signal-to-Noise Ratio (PSNR) is expressed as

\[{\rm psnrv} = 10 \log10(\frac{V_{\rm peak}^2}{\rm MSE}) \]

For float data, \(V_{\rm peak} = 1\);

For interges, \(V_{\rm peak} = 2^{\rm nbits}\), e.g. uint8: 255, uint16: 65535 …

Parameters

  • P (array_like) – The data to be compared. For image, it’s the reconstructed image.

  • G (array_like) – Reference data array. For image, it’s the original image.

  • vpeak (float, int or None, optional) – The peak value. If None, computes automaticly.

  • caxis (None or int, optional) – If P and G are complex-valued but represented in real format, caxis or cdim should be specified. If not, it’s set to None, which means P and G are real-valued or complex-valued in complex format.

  • keepcaxis (int or None, optional) – keep the complex dimension?

  • axis (int or None, optional) – Specifies the dimensions for computing SNR, if not specified, it’s set to None, which means all the dimensions.

  • reduction (str, optional) – The reduce operation in batch dimension. Supported are 'mean', 'sum' or None. If not specified, it is set to None.

Returns

psnrv – Peak Signal to Noise Ratio value.

Return type

float

Examples

import torch as th
import pyaibox as pb

pb.setseed(seed=2020, target='numpy')
P = 255. * np.random.rand(5, 2, 3, 4)
G = 255. * np.random.rand(5, 2, 3, 4)
snrv = psnr(P, G, caxis=1, dim=(2, 3), keepcaxis=True)
print(snrv)
snrv = psnr(P, G, caxis=1, dim=(2, 3), keepcaxis=True, reduction='mean')
print(snrv)
P = pb.r2c(P, caxis=1, keepcaxis=False)
G = pb.r2c(G, caxis=1, keepcaxis=False)
snrv = psnr(P, G, caxis=None, dim=(1, 2), reduction='mean')
print(snrv)

# ---output
[[4.93636105]
[5.1314932 ]
[4.65173472]
[5.05826362]
[5.20860623]]
4.997291765071102
4.997291765071102
pyaibox.evaluation.snrs.snr(x, n=None, **kwargs)

computes signal-to-noise ratio

\[{\rm SNR} = 10*{\rm log10}(\frac{P_x}{P_n}) \]

where, \(P_x, P_n\) are the power summary of the signal and noise:

\[P_x = \sum_{i=1}^N |x_i|^2 \\ P_n = \sum_{i=1}^N |n_i|^2 \]

snr(x, n) equals to matlab’s snr(x, n)

Parameters

  • x (tensor) – The pure signal data.

  • n (ndarray, tensor) – The noise data.

  • caxis (None or int, optional) – If x and n are complex-valued but represented in real format, caxis or cdim should be specified. If not, it’s set to None, which means x and n are real-valued or complex-valued in complex format.

  • keepcaxis (int or None, optional) – keep the complex dimension?

  • axis (int or None, optional) – Specifies the dimensions for computing SNR, if not specified, it’s set to None, which means all the dimensions.

  • reduction (str, optional) – The reduce operation in batch dimension. Supported are 'mean', 'sum' or None. If not specified, it is set to None.

Returns

The SNRs.

Return type

scalar

Examples

import torch as th
import pyaibox as pb

pb.setseed(seed=2020, target='numpy')
x = 10 * th.randn(5, 2, 3, 4)
n = th.randn(5, 2, 3, 4)
snrv = snr(x, n, caxis=1, axis=(2, 3), keepcaxis=True)
print(snrv)
snrv = snr(x, n, caxis=1, axis=(2, 3), keepcaxis=True, reduction='mean')
print(snrv)
x = pb.r2c(x, caxis=1, keepcaxis=False)
n = pb.r2c(n, caxis=1, keepcaxis=False)
snrv = snr(x, n, caxis=None, axis=(1, 2), reduction='mean')
print(snrv)

---output
[[19.36533589]
[20.09428302]
[19.29255523]
[19.81755215]
[17.88677726]]
19.291300709856387
19.291300709856387

Module contents